Welcome! ta-da!
this is a webpage, for pre-cal and AP physics C.
DISCLAIMER: We (Don, Liz, and Dorothy) do not endorse
puppy pitching.
It is mean. Throw a baseball instead.

LAB 2: QUADRATICS IN SPACE OR
PUPPY PITCHING WITH A VENGEANCE
THE PROBLEM:
We have to make a webpage. ( Heh
heh, just kidding )
to
design an experiment that develops the technique of mathematical modeling for
objects moving on Earth.
Materials used:
đ
two
people
đ
one
ball
đ
open
space
đ
video
camera
đ
transparent
graph paper
đ
marker
đ
VCR
đ
TV
đ
time
đ
paper
đ
clothes
“You can’t
think clearly without your clothes on.”
(Margaret Atwood)
We used these materials to collect data.
How we collected data:
ŕ
Play
catch. (For those of you who are not
accustomed to this traditional American pastime, go to
http://espn.go.com/mlb/profiles/profile/3340.html and I’m sure this guy could
give you some tips.)
ŕ
Videotape
a ball being tossed in a game of catch.
ŕ
Tape
a transparent piece of graph paper to a TV screen.
ŕ
Watch
the video in slo-mo (1/30 second increments)
ŕ
Mark
where the ball is with a marker.
ŕ
Label
the points.
ŕ
Make
data to scale.
DATA collected:
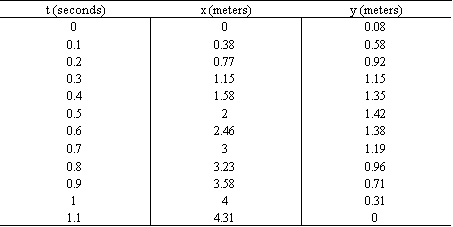
GRAPHS:
X(m) 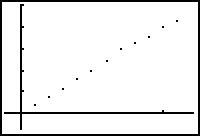 X(m)
X(m) 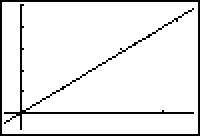
Time(s) Time(s)
y=4.0133x
+ -.0023
Y(m) 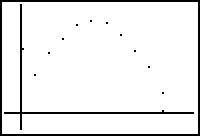 Y(m)
Y(m) 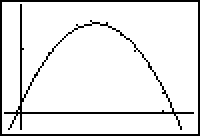
Time(s) Time(s)
y=
-4.4768x^2 + 4.7059x + .1370
Y(m) 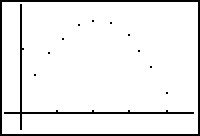 Y(m)
Y(m) 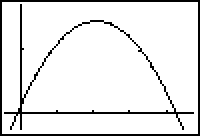
X(m) X(m)
y= -.2963x^2 + 1.2355x + .1240
For those of you who are not
fortunate enough to have Mr. David A. Young as a teacher, these graphs may be
confusing. After our explanation,
however, the information in these graphs should be clear. You may wonder:
Do these graphs have
meaning?
The answer is a resounding
YES! In the time versus x (distance)
graph, the slope of the model is the horizontal velocity of the thrown
ball. In the time versus y (height)
graph, the slope of the model represents the vertical velocity of the same
ball. Finally, the area under the x
(distance) versus y (height) model shows the actual area under the curve of the
thrown ball.
What does the equation at
the bottom of the right-hand graphs mean?
That, Young one, is a
regression. A regression is an equation
of best-fit that is estimated by the calculator for the data points. You can obtain a regression by using the following
steps.
1
Turn
on your TI-83. (If you don’t have a
Graphing Calculator you should get one.)
1
Select
two lists of data that you want an equation for.
1
Hit
the “Stat” button.
1
Choose
“Calc”.
1
Select
the type of regression required for your list of data.
1
Once
on the home screen, enter the two lists that you want separated by a comma and
press enter.
Voila! Un regression! (Vive les Maths)
If physics or pre-calculus
captures your attention, the following web sites will get your engines revving.
http://www.physicsweb.org/resources/dsearch.phtml
http://www.iop.org/cgi-bin/PEERS/search
http://education.ti.com/product/book/73dat.html#author
http://www.colorado.edu/physics/2000/index.pl
http://forum.swarthmore.edu/library/
About the authors:
Don Nix (pre-calculus): Don was
born in a small town on the Alaska-Canada border during the third gold
rush. It was here that began his
adventures in math, counting the gold nuggets that his dad brought in from the
mine as the long days went by. At age
17, Don grew restless of the Miner’s life hitched a ride on an ocean-liner to
Fayetteville. He made his living while
on the boat as a hustler, approaching people with lines such as “Hey, I bet I
know the square root of 573” They would
bet against him and then be amazed that he actually knew! Wow.
When he finally made it to Fayetteville he discovered that there were no
gold mines to work for, so he walked in to Fayetteville HS and asked if he
could be a student for a while. Now, he
is a happy member of David A. Young’s 2000-2001 pre-calculus class.
Dorothy Denny (AP Physics): Before her successful life as an expert
web-page designer/physics prima donna, she lived a simple life in a penthouse
on Broadway, incorporating her master ballet skills into musicals like Cats
and Grease. A scout saw her turn
off gravity in the famous leap she invented known as the “grand jete” and made
an offer she couldn’t refuse. She moved
to Fayetteville where she was blown away.
No, not by the winds, the physics class the scout promised was
everything she hoped for and more. She
doesn’t plan on returning to New York any time too soon, but is thinking about
taking dance up again. The John Powell
Senior Center in Springdale has wooed her into their grips with their $1
ballroom dance hours.
Elizabeth Cox (AP Physics): Unfortunately we couldn’t uncover any of
Elizabeth’s past after the tragic accident on interstate 540. After a deer hit the car in front of her, it
flew up in the air and crashed through the windshield, leaving Elizabeth in
critical condition. She remained in a
coma for three months and when the doctors finally revived her, she had no idea
where or who she was, much less anything that she had experienced before the
class. After months of therapy,
Elizabeth took her first steps and walked straight back into school. Her happiest moment, she says, occured at
1:35 on August 19, 2000, when she assumed the position in David A. Young’s AP
Physics class for the first time. She
slowly reached one hundred percent recovery, physically, but it wasn’t until
after she was able to associate her near death experience with Mr. Young’s
lesson in physics one day that she fully recovered mentally.