
Home | Tips & Tricks | Links | Downloads | Physics | Webmaster
My APPC Webpage
Introduction
Hello everyone, my name is Kevin M. Smith, and welcome to my APPC (Advanced Placement Physics C) webpage. I am a student at Fayetteville High School in Fayetteville, Arkansas, and I am doing this web page as part of a requirement for my APPC class. This is going to be a very simple little page just covering a basic topic of APPC, impulse and momentum. Impulse and Momentum have many applications in the real world. Any time objects come into contact with one another, impulse and momentum are involved. Using these concepts scientists and researchers, for example, can discover many things about a car wreck such as speed, force, direction, etc. These concepts can also be used to develop safer cars.
Impulse and Momentum
- The linear momentum of an object at any time is the product of its mass (m) and velocity (v). So we can write p = m * v where p represents linear momentum, a vector quantity whose direction is that of the velocity vector.
- An impulse is the product of a force (F) and the time interval over which the force lasts (dt). So we can write impulse = F * dt where impulse is also a vector quantity whose direction is that of the force vector.
- An impulse causes a change in momentum, so we can say that impulse = change in momentum or F * dt = m * (Vf - Vi) where Vf = final velocity and Vi = initial velocity. This basically means a force acted upon an object of mass m changing its velocity from Vi to Vf. Furthermore, Newton's Second Law states that force = change in linear momentum / change in time which after being manipulated says F * dt = m * (Vf - Vi) our original formula.
- Linear momentum is conserved. "If the net external force acting on a system of objects is zero, the vector sum of the momenta of the objects will remain constant."
- In collisions and explosions, total momentum before impact = total momentum after impact.
- A perfectly elastic collision has occured when the sum of the kinetic energies of the objects is the same before and after impact.
A problem
-Problem:
A 4.7 kg brick is moving at a speed of 5.6 m/s. How large a force F is needed to stop the brick in a time of .0089 s?
-Answer:
Impulse on brick = change in momentum of brick
F * dt = (m * Vf) - (m * Vi)
F * (.0089 s) = 0 - (4.7 kg) * (5.6 m/s)
F = -2957.303 N
Links
-Principle of Linear Impulse and Momentum
-Watch a Impulse and Momentum Slide Show
-The Impulse-Momentum Equation
-Impulse and Momentum
-Impulse Momentum Theorem
-Intro to Impulse & Momentum
-Mr. Young, you would like this
-Linear momentum and the impulse-momentum theorem
-The linear impulse-momentum relation
Graphs & Data
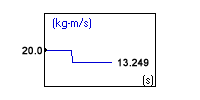
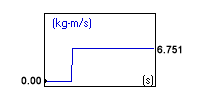
A 10.0 kg ball, ball A, travels along the x axis at 2.0 m/s and hits a 5.0 kg ball, ball B, that is at rest.
Data:
Momentum before impact:
Ball A - 20.00 kg * m/s
Ball B - 0.00 kg * m/s
Momentum after impact:
Ball A - 13.249 kg * m/s
Ball B - 6.751 kg * m/s
You can see that total momentum before is equal to the total momentum after the collision.
Graph:
Ball A Momentum:
Ball B Momentum:
Contacts & Stuff

Click on Mr. Young (my APPC teacher) above to view his APPC web page, or click here to email him. Click here to email me.
Optimized for IE @ 800 X 600




