
Question 1
– Where do these equations come from?
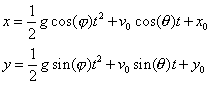
The first approach I am going to make is from an
underlying assumption.
Look around you or read a physics book lying beside
you – gravity is here.
It is the acceleration
that pulls you to the ground every day.
Thus we can
begin by assuming
acceleration equals gravity when an object is in the air.
![]() and remember
and remember ![]()
Therefore ![]() and it follows that
and it follows that ![]()
Now we have ![]() (where c is equal to the initial velocity or
(where c is equal to the initial velocity or ![]() )
)
Since ![]() then it follows that
then it follows that ![]()
And after pushing it through the integration machine
we now have ![]()
As for “c” in this second case when time equals zero
“x” will equal “c” and thus “c” is the initial position or ![]() .
.
So finally by our first method of attack we have ![]() .
.
Since any variable behaves the same as x we have a
second equation ![]() .
.
A second approach to prove the same equations with
the same beginning and end takes down a road less traveled – the geometric
proof.
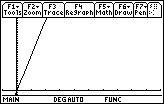
Here we have a representation of what the
acceleration (gravity) vs. time graph looks like
The units on the y-axis are those of acceleration
(m/s/s) and those of the x-axis are time (s).
Notice if we multiply the units together
we get velocity (m/s) which is also the area under
the curve. Thus we take the equation of
y (g) and multiply it times the general time (t)
so that we can define the velocity at any given
time. Thus we have v = gt.
Here we have an interesting predicament.
This is a graph of the velocity vs. time if the
initial velocity is zero (v = gt).
To find distance from this graph we will multiply the
units on the y-axis (velocity – m/s) and the x-axis (s).
By using the triangle area formula ![]() to get distance (m) in terms of time (s). Since the y axis is height and the x axis is
the
to get distance (m) in terms of time (s). Since the y axis is height and the x axis is
the
Base then ![]() . In this particular
case
. In this particular
case ![]() and
and ![]() so therefore
so therefore ![]()
But if the initial isn’t zero but is a constant (we
will use 3 m/s arbitrarily) then we have different graph.
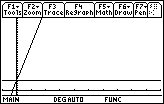
The process continues from the previous example but
we have to account for the area of the rectangle produced by the initial
velocity.
The area of this rectangle is simply the initial
velocity times time. ![]() . Now if we add the
two together we get
. Now if we add the
two together we get ![]()
Here is a graph of the last equation - ![]()
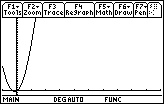
There is a difference between this graph and the
next…
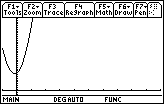
It’s the y-intercept. Since units for the y-axis are meters then this y-intercept is
the initial location of the object in other words the equation must incorporate
an initial position (![]() ).
).
Hereby we have the final equation ![]()
A sub question to address in this section is, “What
will distinguish these two equations?”
This is where our proportion givers come in – the famous
sine and cosine!
Thus far we have assumed gravity as the initial
acceleration for both equations and ![]() for the initial
velocity in both situations. But there
is a difference. Since velocity is a
vector in two-dimensional space it will have two components – one for the x
direction and one for the y direction.
for the initial
velocity in both situations. But there
is a difference. Since velocity is a
vector in two-dimensional space it will have two components – one for the x
direction and one for the y direction.
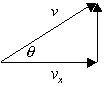
Let’s say
that this is the velocity vector.

Its two components will look like this
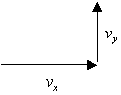
And thereby forming the triangle where ![]() is the angle at which
the velocity is given
is the angle at which
the velocity is given
![]()
With this simple right triangle established we can
use simple trigonometry to define ![]() and
and![]() using
using
following relationships.
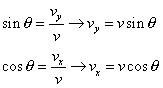
Thus by direction substitution we have the equations
![]()
![]()
Since gravity can be given in different directions we
need these proportion givers for the first term
which produces the final result:
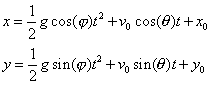
Here are some helpful Math Links:
www.hotmath.org (works problems from specific books)
www.calc101.com (just helpful)
www.sosmath.com (gives some nice proofs)
http://www.sparknotes.com/physics/.dir/ (good with the basics)
http://www.ncsu.edu/felder-public/kenny/home.html
http://www.lib.duke.edu/mathphy/index.htm