Question 2

Mathematical Physics

Question 2 – Where does this equations come from?

The approach I am going to make is from an underlying assumption.

Look around you or read a trig book lying beside you – sine and cosine rule

the world. These two proportions allow us to work with vectors with ease.

First let us consider a vector with length “r” at an angle to the x-axis of .

Its two components will look like this

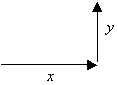
And thereby forming this triangle

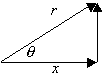
In terms of vector addiction the vector “r” is the sum of the vector “x” and the vector “y”

Now, we can define the particular vectors.

The x vector is equal to x times the x direction or the “i” vector and

the y vector is equal to y times the y direction or the “j” vector.

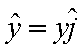
Using basic trigonometry we can discover in even more detail what the x and y vectors actually equal.

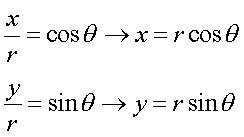
So now we know:

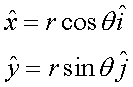
And therefore by direct substitution into the original start of we obtain

Now we come to the final step. In uniform circular motion the angular velocity is equal to

the change in the angle of the change in time (where omega equals angular velocity in units of radians per second)

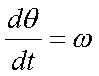
By separating the variables and taking the integral we find that theta equals omega times time.

And thus we finally have our last equation:

Here are some helpful Math Links:

www.hotmath.org (works problems from specific books)

www.sosmath.com (gives some nice proofs)