SIMPLE FACTORING
Have you ever been confused by the factors to factoring? Here is a little help to make you a little less confused.
Suppose you have a simple equation, such as y= x^2 –4. One way to solve this equation would be to factor it. Factoring is an easy, fun way to solve equations. Here is a quick easy example of factoring.
y=(x^2-4) The factors of 4 are (2*2) and (1*4). Now you need to use one set of these factors. (Now remember the standard quadratic equation, which are example is modeled after, is y= ax^2+bx+c, so all the variables will need to be factored, but in our case our variables are just 1,0, and 4. So we have already completed the factoring part.)
y=(x-2)(x+2)
(x-2=y) and (x+2=y) Since the factors are when y=0 then you can solve the two equations and arrive with the answers that x equals 2 and –2.
Graphing and Factoring Combine
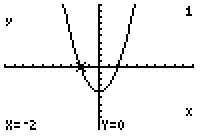
Another way to solve an equation while still using factors is to graph it. Take the simple equation used earlier y=(x^2-4). Put this equation into the y= part in your calculator. (Figure One). Then you will graph the equation. (Figure Two) Looking at the window (Figure Three), the x-intercepts, which are the factors in the equation or where y equals zero are 2 and -2 just as we found earlier (Figures Four and Five).
Fig.1 Fig.2
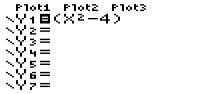
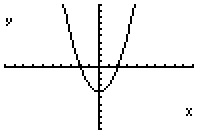
Fig.3 Fig.4
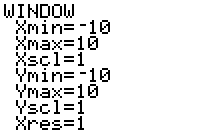
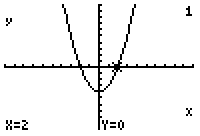
Fig.5
A Little More
Take the equation, y=2x^2-x-3 First you must factor this equation or the numbers in the equation. The factors of 2 are (1*2) and the factors or 3 are (1*3). First of all, which of these numbers combined will equal –1 from the y=2x^2-1x-3. Take one number from each factor group to find this negative one. Taking the two from the first pair and subtracting it from the three in the second pair will get a negative one. So now you know that the two and three will be paired together and the two ones will be paired together.
Y=(2x-3)(x+1)
Remember that to get a negative number you have to multiply a negative number and a positive number. So one of the factors will be negative and one will be positive. Since the factors are the x-intercepts, that means they occur when y=0.
Solve the equation:
2x-3=0 x=3/2
x+1=0 x=-1
Once again we will use graphing to check the answers that we found. Take the simple equation used earlier y=(2x2-x-3). Put this equation into the y= part in your calculator. (Figure One). Then you will graph the equation. (Figure Two) Looking at the window (Figure Three), the x-intercepts, which are the factors in the equation or where y equals zero are -1 and 3/2 just as we found earlier (Figures Four and Five).
Fig. 1
Fig. 2
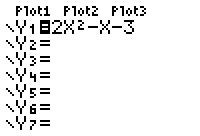
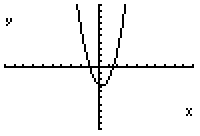
Fig. 3 Fig. 4
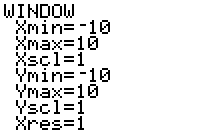
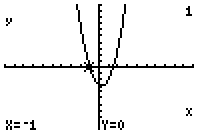
Fig. 5
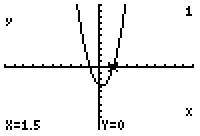
History of Factoring
Factoring was created as another way to solve equations. People realized that another way to write an equation was through using the x-intercepts. You could use these intercepts to solve the equation or rewrite it.
Related Sites
- http://www.salesledgerfinance.com/
- http://www.commonname.com/english/search/PSEngine.asp
- http://www.sosmath.com/algebra/algebra.html
- http://www.ontko.com/~rayo/primes/
- http://www.commonname.com/english/search/PSEngine.asp?userid=0&engine=lycos&query=FactoringSites
- http://www2.hawaii.edu/suremath/opportunityA.html
- http://www.math.niu.edu/~rusin/known-math/index/26-XX.html
- http://www.utexas.edu/cc/docs/math01.html
A Little Something About the Author
My name is Elizabeth Watkins. I am a 2002 graduating senior and a PreCalculus student. I enjoy riding horses and anything related to the water: skiing, swimming, boating, etc. I created this factoring website because I enjoy factoring and factoring is a very important topic that math students will use throughout their math careers. I think it is important for all future math students to have a good factoring foundation. My e-mail address is
Liza1712@aol.com. This is a picture of the book from PreCalculus that helped to change my life.
