Welcome to my web page for PreCalculus. Let me introduce myself. My name is Matt Hamblen. I'm a senior at Fayetteville High School, and am currently enrolled in a PreCalculus program. I play baseball, listen to music, and sit at home doing math problems in my spare time. This web site has been created in order to provide information to you, the reader, on how to use your TI-89 calculator to find the derivative of an equation.

The first thing you must do is purchase a TI-89 calculator. This will cost you close to $150.00, but it is well spent and worth every cent of it. Some calculators come with a graph link so that you can hook your calculator into Port 1 on the back of the computer, but some (as in my case) do not. Make sure to look into this at the store because it is imperative that you have one. This way, you will be able to provide documentation of your answers without ever having to write anything.

Finding the derivative of an equation allows you to know the equation (and therefore slope) of a line that correlates with a certain point on a curved graph. For example, if you were given the equation -1.5x^2+2.5x-7, you would know that where h=0 the slope of the tangent line is m=-3x+2.5.

I will now teach you how to find the derivative by hand, so that you will know how much easier the TI-89 makes the problem. The formula for finding derivatives is m=(f(x+h)-f(x))/(x+h-x) Going back to my previous example, we are going to find the derivative of f(x)=-1.5x^2+2.5x-7.

The first step is to plug all of your numbers into their corresponding letters in the equation:
(-1.5(x+h)^2+2.5(x+h)-7+1.5x^2-2.5x+7)/h
You then cross out whatever cancels each other out:
(-3hx-1.5h^2+2.5h)/h
You will be left with a quadratic equation, so you can factor out the common term; h:
(h(-3x-1.5h+2.5))/h
Obviously, the next step is to cancel out the h:
-3x-1.5h+2.5
You can then set the h to 0 to find the derivative in terms of f(x):
-3x+2.5

The graph of this equation with its tangent derivative line looks like this from the viewpoint of a TI-89:


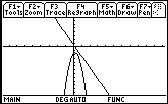
And now for the fun and easy part, I will show you how the TI-89 solves derivatives the easy way.
From the home screen on your calculator, hit the F3 key, this will bring the pull down for the "Calc" category.

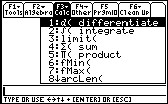
Scroll down to the 1st option "d(differentiate" and press enter, or you can just push the number 1 on your key pad.
It will show up as "d("

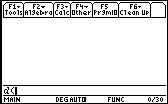
Now, type in the equation after "d(" in its quadratic form. After you have typed it in, put a comma and "x" and then close the parenthesis.

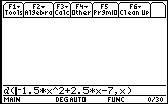
Press enter and watch as your TI-89 processes and solves the derivative.


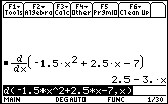
You can transfer all the screens by going into the "get screen" category of the TI-89 program that is on the school's computer systems.
You should now be having fun with derivatives. The example for this web page was provided by Mr. Young's First Semester "Slope Quiz" (which I passed).

Here are some additional links that should help you out as you explore the exciting world of derivatives:
David A. Young's Web Site
Texas Instrument's Web Site
University of Akron's "E-Calculus"
An Introduction to the Calculus of Variation
Calc 101 Web Page
The Calculus Haters Home Page
Graphics for the Calculus Classroom
My E-mail address