Definition:
The logarithmic function (with base b), written f (x)= logb (x), is the inverse of the exponential function bx.
Use for logarithmic functions…
· Solving exponential functions
· Turn multiplication into addition
History: Before the invention of the calculators, first tables of logarithms and then slide rules based on logarithms were used as an aid to multiplication.
logb(bx) = blogbx
= x.
In other words, y = logbx if and only if
x = by.
Example: log2 16 = log2 24 = 4
log5 (1/25) = log5 5-2 = -2
The Algebra of Logarithms
Here are the main rules for manipulating logarithms:
- logbxy = logbx + logby.
- logbxy = y logbx.
- logb1=0.
- logb0 is undefined (or -infinity).
- logbx = (logbc)logcx.
The last rule shows that all logarithmic functions are the same except for a constant multiple.
Graph
Graphs of exponential functions are pretty easy to sketch, for they all go through the point (0,1) and are increasing everywhere if the base is larger than 1, and decreasing everywhere if the base is between 0 and 1. A logarithmic function and its inverse have graphs that are reflections of each other through the line y = x. The applet below shows the graphs that are reflections of each other through the line y=x.
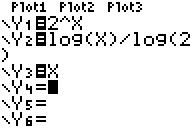 In y2
you can see how you have to type in log2x to get the right graph.
In y2
you can see how you have to type in log2x to get the right graph.
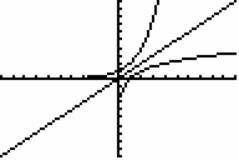
Properties of logarithmic functions
- The domain of a logarithmic function is (0,inf). That means logbx is only defined for x>0. It is because the range of every exponential function is (0,inf.), and logarithmic functions are inverses of exponential functions.
- Since
all the graphs of exponential functions contain the point (0,1), the
graphs of all logarithmic functions contain the point (1,0), the
reflection of (0,1) in the line y = x. Logb 1 = 0 for all b.
- If the base b is larger than 1, the function logb is increasing everywhere.. If the base a is between 0 and 1, then the function logb is increasing everywhere.
- Because a1 = a, logarithmic identity1 above implies logb b = 1
The exponential
function and the natural logarithm
The
most important exponential function is ex, or also called the exponential
function. It follows that its inverse, the logarithm with base e, is the most
important of the logarithmic functions. The logarithm with base e is called the
natural logarithm, and it is denoted ln().
- The natural logarithm of x = ln x = loge b
The natural logarithm is the one, which has the nicest purely mathematical properties and is the one, which we use almost exclusively in calculus
- The common logarithm of x = log x = log10 x
Many scientific calculators have buttons devoted to the natural logarithm and the logarithm base 10
The History of logarithms by Wikipedia
“Jaina
mathematicians in ancient
In the
17th century, Joost Bürgi, a Swiss clockmaker in the employ of the Duke of
Hesse-Kassel, first discovered logarithms as a computational tool; however he
did not publish his discovery until 1620. The method of logarithms was first
publicly propounded in 1614, in a book entitled Mirifici Logarithmorum
Canonis Descriptio, by John Napier, Baron of Merchiston in
At
first, Napier called logarithms "artificial numbers" and
antilogarithms "natural numbers". Later, Napier formed the word logarithm,
a portmanteau, to mean a number that indicates a ratio: λoγoς (logos)
meaning ratio, and αριθμoς (arithmos)
meaning number. Napier chose that because the difference of two logarithms
determines the ratio of the numbers for which they stand, so that an arithmetic
series of logarithms corresponds to a geometric series of numbers. The term
antilogarithm was introduced in the late 17th century and, while never used
extensively in mathematics, persisted in collections of tables until they fell
into disuse.
Napier
did not use a base as we now understand it, but his logarithms were, up to a
scaling factor, effectively to base 1 / e.
For interpolation purposes and ease of calculation, it is useful to make the
ratio r in the geometric series close to 1.
Napier chose r = 1 − 10 − 7 =
0.999999, and Bürgi chose r = 1 + 10 −
4 = 1.0001. Napier's original logarithms did not have log 1 = 0
but rather log 107 = 0. Thus if N is a number and L
is its logarithm as calculated by Napier, N = 107(1
− 10 − 7)L. Since ![]() is approximately 1 / e,
L is approximately 107log1
/ eN / 107. “
is approximately 1 / e,
L is approximately 107log1
/ eN / 107. “
Graph
Let us look at a “real life” problem in which you need logarithmic functions:
Tim says that the temperature on the probe rises constantly when you use it for measuring you body temperature. Smart Smith says that it will create a logarithmic function…
He measured the temperature of his hand and got the following data, starting at 22.55 degrees Celsius.
|
Time (sec) |
Temp (Celsius) |
|
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 135 140 145 150 155 160 165 170 175 180 |
22.55 26.547 29.619 31.778 33.389 34.441 35.404 36.18 36.472 37 37 37.059 37.059 37.059 37.059 37.062 37.062 37.062 37.062 37.063 37.063 37.07 37.077 37.077 37.077 37.077 37.077 37.08 37.08 37.081 37.081 37.082 37.082 37.082 37.082 37.082 37.082 |
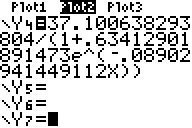

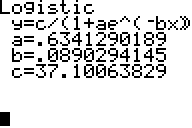
He did the Logistic regression and got the graph. He was right, it is a logarithmic function. Who would have thought so...?
 In
the time before Calcuators they had books full of common logarithms. This one
it from the 20th century.
In
the time before Calcuators they had books full of common logarithms. This one
it from the 20th century.
About me:
I am Konstantin Koerner and senior at
Links:
More about logarithms at Wikipedia